Software
mcMandelbrot
Multi-core interactive visualization of the Mandelbrot set.
The mcmandelbrot package bundled with AsynQueue provides a usage example and a cool little app as well. It runs under the command line or as a web server (port 8080) via twistd. See mcmandelbrot.main and mcmandelbrot.html.
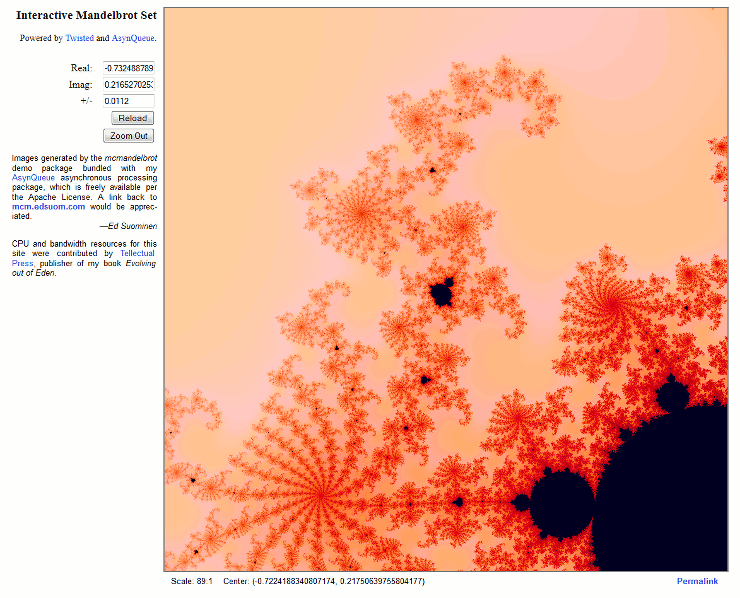
I currently have an online demonstration running on my multi-core virtual private server at mcm.edsuom.com. Take a look. You can go right to the image pictured here, and click for further detail, via this direct link.
After installing AsynQueue and its primary dependency, the venerable Twisted asynchronous framework for Python, you can get your multcore CPU cranking away doing asynchronous multiprocessing. You’ll have a console entry point for mcmandelbrot. Give it a try and see what asynchronous multiprocessing can do!1
Row, Row, Row Your Cores . . .
Each row of the PNG file generated by the Runner object is computed on a subordinate Python interpreter. The heavy lifting is done by the MandelBrotValuer object, particularly this bit of inline C code:
int j, zint;
int N = km;
signed char kx, ky;
double xk, yk;
for (j=0; j<Nx[0]; j++) {
// Evaluate five points in an X arrangement including and around the
// one specified by X1(j) and ci
zint = eval_point(j, km, X1(j), ci);
Z1(j) = zint;
kx = -1;
ky = -1;
while ((zint < km) && (kx < 2)) {
xk = X1(j) + kx * qd;
while ((zint < km) && (ky < 2)) {
yk = (double)ci + ky * qd;
zint = eval_point(j, km, xk, yk);
Z1(j) += zint;
ky += 2;
}
kx += 2;
}
if (zint == km) {
// A no-escape evaluation at one point in the X is treated
// as if there were no escape at any point in the X
Z1(j) = 5*N;
}
}
For five points in an X configuration centered at one pixel of the image, this code does the fundamental calculation for membership in the Mandelbrot set: periodicity of z = z2 + c. If z remains in a stable region of the complex plane or revisits the same point, it is in the Mandelbrot set. The pixel will be assigned a maximum iteration value, which will be mapped to a nearly black, very deep blue. No further points in the X need be computed.
Otherwise, computation proceeds with the other points. The pixel value will be the sum of all iterations required for z to break out of the stable region for each point in the X.
The Mandelbrot calculation is done in the C function eval_point.2 It calls another function region_test to quickly determine membership for points lying within the two biggest “lakes” of the Mandelbrot set.3
Here’s the code for those two functions:
bool region_test(double zr, double zr2, double zi2)
{
double q;
// (x+1)^2 + y2 < 1/16
if (zr2 + 2*zr + 1 + zi2 < 0.0625) return(true);
// q = (x-1/4)^2 + y^2
q = zr2 - 0.5*zr + 0.0625 + zi2;
// q*(q+(x-1/4)) < 1/4*y^2
q *= (q + zr - 0.25);
if (q < 0.25*zi2) return(true);
return(false);
}
int eval_point(int j, int km, double cr, double ci)
{
int k = 1;
int N = km;
double zr = cr;
double zi = ci;
double zr2 = zr * zr, zi2 = zi * zi;
// If we are in one of the two biggest "lakes," we need go no further
if (region_test(zr, zr2, zi2)) return N;
// Periodicity-testing variables
double zrp = 0, zip = 0;
int k_check = 0, N_check = 3, k_update = 0;
while ( k < N ) {
// Compute Z[n+1] = Z[n]^2 + C, with escape test
if ( zr2+zi2 > 16.0 ) return k;
zi = 2.0 * zr * zi + ci;
zr = zr2 - zi2 + cr;
k++;
// Periodicity test: If same point is reached as previously,
// there is no escape
if ( zr == zrp )
if ( zi == zip ) return N;
// Check if previous-value update needed
if ( k_check == N_check )
{
// Yes, do it
zrp = zr;
zip = zi;
// Check again after another N_check iterations, an
// interval that occasionally doubles
k_check = 0;
if ( k_update == 5 )
{
k_update = 0;
N_check *= 2;
}
k_update++;
}
k_check++;
// Compute squares for next iteration
zr2 = zr * zr;
zi2 = zi * zi;
}
}
Color Mapping
The values are inverted, i.e., subtracted from the maximum value, so that no-escape points (technically, the only points that are actually in the Mandelbrot Set) have zero value and points that escape immediately have the maximum value. This allows simple mapping to the classic image with a black area in the middle. Then they are scaled to the 0.0-1.0 range, and an exponent is applied to emphasize changes at shorter escape times. Finally, they are mapped to RGB triples and returned. Here’s where it happens, in calls to the MandelBrotValuer object:
def __call__(self, crMin, crMax, N, ci):
"""
Computes values for I{N} points along the real (horizontal) axis
from I{crMin} to I{crMax}, with the constant imaginary
component I{ci}.
@return: A Python B-array I{3*N} containing RGB triples for an
image representing the escape values.
"""
qd = 0.25 * (crMax - crMin) / N
x = np.linspace(crMin, crMax, N, dtype=np.float64)
z = self.computeValues(N, x, ci, qd)
# Invert the iteration values so that trapped points have zero
# value, then scale to the range [-1.0, +1.0]
z = 2*self.scale * (5*self.N_values - z) - 1.0
# Transform to emphasize details in the middle
z = self.transform(z, self.steepness)
# [-1.0, +1.0] --> [0.0, 1.0]
z = 0.5*(z + 1.0)
# Map to my RGB colormap
return self.cm(z)
The color mapping was tricky, because there are some very small gradations between iteration values when you zoom in on fine details of the Mandelbrot set. I wanted to keep it nearly monotonic and didn’t want to be using different color maps for different regions. Here’s what I came up with:
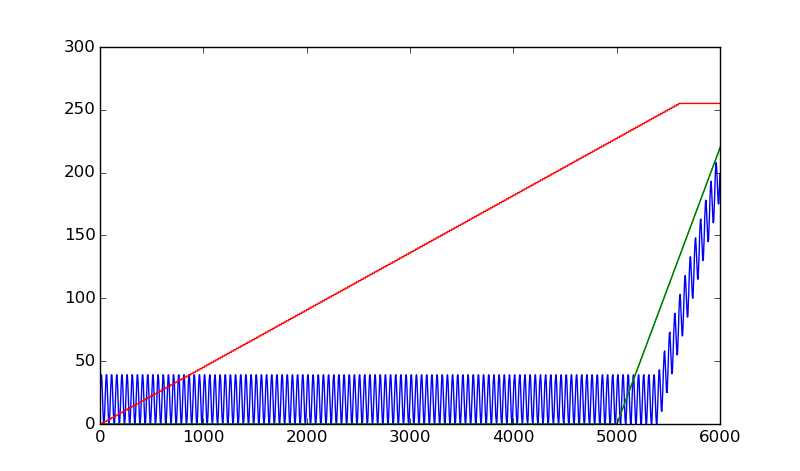
Adding a little bit of periodicity to the blue component has a nice effect, showing small changes without upsetting the overall reddish/gold increasing-temperature color scheme.
Asynchronous to Blocking, and Back Again
A ProcessQueue dispatches all the row computations and assembles the byte arrays of RGB image rows as they come back in. It presents the rows to a blocking png.Writer object as a regular row iterator, in order, via the magic of asynqueue.threads.Filerator.
Here’s the compute method of the Runner object that does all that:
@defer.inlineCallbacks
def compute(self, fh, xSpan, ySpan, dCancel=None):
"""
Computes the Mandelbrot Set under C{Twisted} and generates a
pretty image, written as a PNG image to the supplied file
handle I{fh} one row at a time.
@return: A C{Deferred} that fires when the image is completely
written and you can close the file handle, with the number
of pixels computed (may be a lower number than expected if
the connection terminated early).
"""
def f(rows):
try:
writer = png.Writer(Nx, Ny, bitdepth=8, compression=9)
writer.write(fh, rows)
except Exception as e:
# Trap ValueError caused by mid-stream cancellation
if not isinstance(e, StopIteration):
if "rows" not in e.message and "height" not in e.message:
raise e
crMin, crMax, Nx = xSpan
ciMin, ciMax, Ny = ySpan
# We have at most 5 calls in the process queue for each worker
# servicing them, to allow midstream canceling and interleave
# parallel computation requests.
ds = defer.DeferredSemaphore(5*self.N_processes)
p = OrderedItemProducer()
yield p.start(f)
# "The pickle module keeps track of the objects it has already
# serialized, so that later references to the same object won't be
# serialized again." --Python docs
for k, ci in enumerate(np.linspace(ciMax, ciMin, Ny)):
# "Wait" for the number of pending calls to fall back to
# the limit
yield ds.acquire()
# Make sure the render hasn't been canceled
if getattr(dCancel, 'called', False):
break
# Call one of my processes to get each row of values,
# starting from the top
d = p.produceItem(
self.q.call, self.mv, crMin, crMax, Nx, ci,
series='process')
d.addCallback(lambda _: ds.release())
yield p.stop()
defer.returnValue(Nx*(k+1))
See that f(rows sub-function inside the method? It is called by the OrderedItemProducer with what the png.Writer object thinks is a regular blocking iterator, rows. But in Twisted land, rows is something produced by the asynchronous, deferred results from calls to the ProcessQueue! And the blocking writes to fh are translated back out to Twisted land, too.
As far as the Twisted reactor is concerned, nothing is blocking. All the underlying thread-locking primitives are called in the reactor thread as appropriate to avoid race conditions.
Intelligently buffering the asynchronous results and iterating them in a proper sequence, using a thread to both yield and accept blocking iterations, allows the use of a third-party library that wouldn’t ordinarily play nice with Twisted. There’s a lot going on to make that happen, and it all works beautifully.
License
Copyright (C) 2006-2007, 2015 by Edwin A. Suominen, http://edsuom.com/:
See edsuom.com for API documentation as well as information about Ed's background and other projects, software and otherwise. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
Notes
-
You’ll probably need to install a few other dependencies, including numpy and pypng. I didn’t make them requirements in the setup.py file of AsynQueue because they are only needed for mcmandelbrot, and it’s just a demo package bundled with the main one. They are all easy enough to identify from error messages and then install with pip install. ←
-
Adapted from Ilan Schnell’s iterations function at https://svn.enthought.com/svn/enthought/Mayavi/branches/3.0.4/examples/mayavi/mandelbrot.py. ←
-
See http://en.wikibooks.org/wiki/Fractals/Iterations_in_the_complex_plane/Mandelbrot_set. ←

